China and Nepal have announced Mount Everest is 0.86 m taller than the 8,848 m accepted globally so far.

Try this PYQ:

Q.When you travel to the Himalayas, you will see the following:

1. Deep gorges
2. U-turn river courses
3. Parallel mountain ranges
4. Steep gradients causing land-sliding

Which of the above can be said to be the evidences for the Himalayas being young fold mountains?

(a) 1 and 2 only

(b) 1, 2 and 4 only

(c) 3 and 4 only

(d) 1, 2, 3 and 4

Scaling a mountains’ height

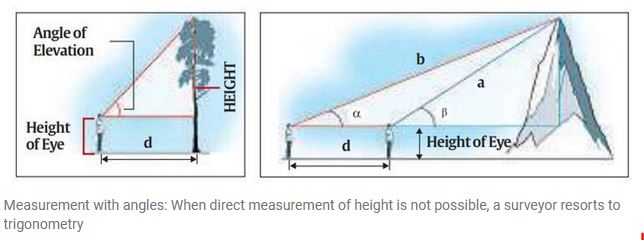
• The basic principle that was used earlier is very simple and uses  only trigonometry which most of us are familiar with, or at least can recall.
• There are three sides and three angles in any triangle. If we know any three of these quantities, provided one of them is a side, all the others can be calculated.
• In a right-angled triangle, one of the angles is already known, so if we know any other angle and one of the sides, the others can be found out.
• This principle can be applied for measuring the height of any object that does not offer the convenience of dropping a measuring tape from top to bottom.

Accuracy issues

• For small hills and mountains, whose top can be observed from relatively close distances, this can give quite precise measurements.
• But for Mount Everest and other high mountains, there are some other complications.
• These again arise from the fact that we do not know where the base of the mountain is.

Measuring against sea level

• Generally, for practical purposes, the heights are measured above mean sea level (MSL). Moreover, we need to find the distance to the mountain.
• This is done through a painstaking process called high-precision levelling. Starting from the coastline, we calculate step by step the difference in height, using special instruments.
• This is how we know the height of any city from mean sea level.

Adjusting gravitation anomaly

• But there is one additional problem to be contended with — gravity. Gravity is different in different places. It means that even sea level cannot be considered to be uniform at all places.
• So, the local gravity is also measured to calculate the local sea level. Nowadays sophisticated portable gravitometers are available that can be carried even to mountain peaks.

Technology solutions

• These days GPS is widely used to determine coordinates and heights, even of mountains.
• But, GPS gives precise coordinates of the top of a mountain relative to an ellipsoid which is an imaginary surface mathematically modelled to represent Earth.
• This surface differs from the mean sea level. Similarly, overhead flying planes equipped with laser beams (LiDAR) can also be used to get the coordinates.

How accurate are China/Nepal’s apprehensions?

• Considering that during 1952-1954, when neither GPS and satellite techniques were available nor the sophisticated gravimeters, the task of determining the height of Mount Everest was not easy.
• Nepal and China have said they have measured Mount Everest to be 86 cm higher than the 8,848 m that it was known to be.
• But these have been explained in terms of geological processes that might be altering the height of Everest. The accuracy of the 1954 result has never been questioned.
• Most scientists now believe that the height of Mount Everest is increasing at a very slow rate. This is because of the northward movement of the Indian tectonic plate that is pushing the surface up.
• Big earthquake, like the one that happened in Nepal in 2015, can alter the heights of mountains. Such events have happened in the past.

Get an IAS/IPS ranker as your 1: 1 personal mentor for UPSC 2024

Attend Now